Reconstruction of the Atanasoff-Berry Computer

John Gustafson

Iowa State University, Ames, Iowa, USA

Abstract

The Atanasoff-Berry Computer (ABC) introduced electronic binary logic in the late 1930s. It was also the first to use dynamically refreshed capacitors for storage, as in current RAM. Perhaps most astonishing is that it was parallel, supporting up to 30 simultaneous operations. Yet, it had far fewer parts than the serial computers that followed it in the 1940s. Atanasoff and Berry completed the computer by 1942, but it was later dismantled. Only a few parts of the original computer remain. In 1994, a team of engineers, scientists, and students at Iowa State University/Ames Laboratory began rebuilding the ABC. We demonstrated the functioning replica on October 8, 1997.

In this paper, I describe the computer in modern computer architectural terms to facilitate technology comparison. While patent applications, purchase orders, and photographs gave much information for the reconstruction, a number of mysteries about the computer were solved only as a result of the effort to reproduce it. The answers to those mysteries are presented here for the first time.

1. Atanasoff’s Motivation

John Atanasoff was a physicist by training, whose interests included molecular spectra and crystallography. As a graduate student, he often found it necessary to solve systems of linear equations by hand, and as a professor he had advisees similarly engaged in the arduous process. He noted:

Since an expert [human] computer takes about eight hours to solve a full set of eight equations in eight unknowns, k is about 1/64. To solve twenty equations in twenty unknowns should thus require 125 hours… The solution of general systems of linear equations with a number of unknowns greater than ten is not often attempted.

—Computing Machine for the Solution of large Systems of Linear Algebraic Equations

J. Atanasoff, 1940

Alt made a strikingly similar eight years later [6]:

…13 equations, solved as a two-computer problem, require about 8 hours of computing time. The time required for systems of higher order varies approximately as the cube of the order. This puts a practical limitation on the size of systems to be solved… It is believed that this will limit the process used, even if used iteratively, to about 20 or 30 unknowns.

—A Bell Telephone Laboratories Computing Machine

F. Alt, 1948

In the evolution of automatic computing, solving a system of linear equations was the original “Grand Challenge.” Trigonometric functions and logarithms could be tabled, and mechanical desktop calculators such as the 10-decimal Marchant could handle short sequences of + – × ÷ operations. Gaussian elimination had order N³ operations for N unknowns, however, and this made manual methods unscalable. Atanasoff listed his target applications [6], which look much like the typical workload at a modern supercomputer center:

Multiple correlation

Curve fitting

Method of least squares

Vibration problems including the vibrational Raman effect

Electrical circuit analysis

Analysis of elastic structures

Approximate solution of many problems of elasticity

Approximate solution of problems of quantum mechanics

Perturbation theories of mechanics, astronomy, and the quantum theory

Atanasoff struggled for years to find a physical way to perform arithmetic that was digital instead of analog. He appears to have been the first to draw the distinction between the two, and to coin the term “computer” for a mechanical device. He thought about parallel processing much the way we do now, in that he considered connecting 30 commodity devices (mechanical Monroe calculators) to attain the necessary speed [1]. He discarded this approach as clumsy and error-prone. In late 1937 [5], he suddenly made the mental leap that provided him with what he was seeking while at a roadhouse near the Mississippi River. He jotted four principles [2] on a napkin, paraphrased here:

Electricity and electronics, not mechanical methods

Binary numbers internally

Separate memory made with capacitors, refreshed to maintain 0 or 1 state

Direct 0-1 logic operations, not enumeration

On the other side of the world, the designs of Konrad Zuse were independently paralleling those of Atanasoff, but the Zuse designs were mechanical or relay-based [7]. While the Zuse automatons were less advanced than the ABC in switching and storage technology, they were far ahead of their time in having full floating point arithmetic and a real instruction set.

By 1940, Atanasoff and graduate student Clifford Berry had taken the above ideas to practice. I will present details of the design, including features not previously explained in the literature on the ABC [1, 2, 4, 5, 6].

2. Block Diagram

Figure 1 shows an overview of the ABC. It uses terminology more like that for modern computers than like that of the original documentation. Terms like “keyboard abacus” have little meaning for present-day computer engineers.

Figure 1. ABC Block Diagram

Because the add-subtract modules could be used for base conversion (both directions) as well as vector addition and subtraction, the total vacuum tube count was very low: about 300 for the entire machine. Much of this economy is the result of operating on only one bit of each number at a time, keeping the carry/borrow bit in a capacitor for use in the next cycle. The 60 Hz line power served as the system clock; one 50-bit number could be added or subtracted in 5/6 of a second, with 1/6 of a second idle time.

The separation of memory from processing is one we now take for granted. On analog computers, there is no such separation. Atanasoff and Zuse independently made the same profound breakthrough in realizing the need for separate “memory,” as Atanasoff anthropomorphically called it. One of the few news releases of the Iowa State College (now Iowa State University) about the ABC used the headline, “MACHINE ‘REMEMBERS’.”

3. Physical Design

The ABC is much smaller than the other early computers. The original dimensions were 1.5 m long, 0.91 m high, and 0.91 m wide. The seemingly minor decision about the width had much to do with the eventual destruction of the original device.

It was constructed in the basement of the physics building at ISU, which at the time was an open area interrupted only by support pillars. The basement was later finished with poured concrete walls and standard doors; the standard door width is 0.84 m. Hence, the computer was boxed in. After Atanasoff left ISU for Maryland, the ABC was seen only as an orphaned device taking up otherwise useful space. Since its frame was welded angle iron, the only way to remove it from the room was to cut it apart with a hacksaw. I feel we have most of the answer to the question: Why was the ABC destroyed? The answer is that it was 0.07 m too wide to go through the door. In reconstructing the ABC, we made one practical modification: we narrowed the frame enough so we would be able to go through a standard door.

Figure 2 shows the reconstructed ABC, using a camera angle similar to that of the historical pictures of the original.

Figure 2. The ABC Replica

The weight of the machine is about 750 pounds. It rolls on four heavy-duty casters, with the weight and maneuverability of an upright piano. Like a piano, the ABC must be “tuned” after moving to make sure that the timings of brush-triggered events are still within tolerance. The remarkable thing, of course, is that any such antique computer would be so portable. ABC successors such as the ENIAC and the Mark I were notorious for filling rooms with bulky, heavy equipment. The ABC replica has logged thousands of miles in its tours around the country, using a protective crate and a truck specialized for moving sensitive scientific equipment, and it remains functional.

We wondered about the power consumption of the system, but have found that the total power drawn does not exceed 1000 W. The heat generated by the tubes is barely perceptible if one stands near the computer. There is no need for fan-driven cooling; what heat is generated disappears by convection in the open design.

The ABC uses ordinary U.S. line power, 117 VAC, 60 Hz. It was not designed with safety in mind; the two main bus voltages are +120 V and –120 V, and in many places on the computer large, unshielded surfaces at these voltages are separated from ground by a few centimeters. With protective covers removed, the rotating memory drums could easily snag loose clothing. We do not expect to operate the computer on a routine demonstration basis, but to rely on videotapes and simulations of its operation.

The physical design is true to that of the original, with the exception of the slightly narrower width and slightly more modern wire (plastic coated instead of cloth coated, coaxial shielding instead of twisted pairs). The contact brushes are the same IBM part used in 1939. The phenolic resin cylinders that hold the memory appear to be the same stock as used by Atanasoff.

The total amount of wire in the ABC is about 1600 m, and almost all connections are soldered. The manual effort required for the wiring (and correction of wiring errors) was probably the single largest part of the cost of the reconstruction itself. We discovered an advantage of the original’s cloth-covered wire when we found that the soldering irons had melted some of the replica wire’s plastic sheathing enough to cause short circuits in shielded cables.

4. Finding 1939 Vintage Parts

People often ask us, “Where did you get the vacuum tubes? Weren’t they difficult to find?” Several suppliers stock vacuum tubes of the correct type. An Army-Navy warehouse in California supplied us with enough tubes for the entire ABC plus a few spares. About half the tubes tested were gassy, but the remainder worked; most of those that worked were still within design specifications. Finding vacuum tubes was by no means our biggest challenge.

It was much more difficult to find a proper synchronous motor to drive the rotating drums. Modern synchronous AC motors can synchronize on the positive or the negative part of the AC power cycle; in 1939, they were wound to synchronize on only the positive part. This does not affect any of the computational logic, but it does affect the base-2 card writer and base-2 card reader. Cards written while synchronized to one phase of the motor will not read properly if the machine becomes synchronized to the opposite phase (as can happen whenever the machine is turned off and back on).

In building add-subtract modules, we found the circuits very demanding of precise resistor values. We have evidence that Berry hand-selected resistors from bins until he found ones that worked, and we attempted the same tactic. In measuring a collection of ±10% resistors, we discovered the following distribution about the nominal value:

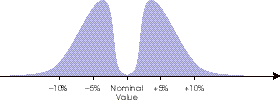
Figure 3. Distribution of ±10% Resistor Values

Apparently, the manufacturer had already segregated the resistors close to nominal value. Hence, we found it necessary to use 1% tolerance resistors.

5. Arithmetic and Rounding Error

The ABC arithmetic is 50-bit binary, 2’s complement integer arithmetic. There are no tests for overflow. There is also no rounding when it divides numbers by two via shifting. While this may initially seem to pull values toward zero with every operation, closer examination shows that the Gaussian elimination process causes the data to alternate from positive to negative values, and thus the truncation of bits is balanced on the average. After order N iterations of the subtract-shift process, the values will be off by about √N bits in the least significant place.

The simple examples in Berry’s thesis describing the use of the ABC use linear equations with integer coefficients, avoiding discussion of roundoff error. Now that the reconstruction has allowed us to experiment with the computer, it is obvious that Atanasoff and Berry intended to scale all input values so they would occupy the most significant bits in the 50-bit words. The √N bits of error in the least significant place would be negligible for well-posed problems. With the exception of circuit analysis, the physical applications Atanasoff had in mind tend to produce positive definite matrices for which the ABC could easily generate answers correct to ten or more decimals accuracy.

6. A Stumbling Block: The ABC Mass Storage Scheme

Atanasoff and Berry knew they would need to record intermediate results somehow. The refreshed-memory storage was only sufficient to hold two rows of the system of equations (up to 29 variable coefficients plus the right-hand constant coefficient). As rows are altered by the Gaussian elimination scheme, they would have to be stored and reloaded later.

Reading the intermediate answers manually by conversion to decimal was out of the question. It could take up to two minutes to convert each 50-bit binary number to a 15-decimal number on the odometer readout, which also had the inconvenient side effect of destroying the original 50-bit number.

A mechanical cardpunch was considered, but would have brought in all the usual disadvantages of mechanical computation that Atanasoff was seeking to eliminate. He wanted an electronic solution. (Magnetic storage did not evolve until after World War II.)

The solution he and Berry came up with was to use high-voltage arcs to burn holes in paper; a hole for a “1” and no hole for a “0.” Berry refers to the paper as “dielectric material.” It appears that paper was the only material ever used. The thyratron tubes visible on the left side of the ABC provided the high-voltage pulse to create the arcs. Reading the cards was done by passing the card between electrodes at a lower voltage than that used to burn the card, and with blunt electrodes instead of pointed ones to allow for small differences in alignment between reading and writing. The idea is that the arc will form in the card reader if there is a hole in the card, but the dielectric strength of the paper will prevent this if there is no hole.

Note that there are at least five variables to adjust for this method to work:

1) The voltage used to write

2) The voltage used to read

3) The thickness of the paper

4) The spacing of the electrodes used to write

5) The spacing of the electrodes used to read.

From telephone discussions with Clifford Berry’s widow, we learned that Berry found the optimum paper to be Strathmore No. 2. This paper is no longer manufactured, but we know it was thicker than ordinary bond paper and not as thick as IBM card stock. A too-thin paper would buckle in the mechanism and would not prevent arbitrary arcs in the reading of the card; a too-thick paper might prevent arcs in the writing of the card, or snag on the electrodes. Unlike the rest of the ABC, this technology was not prescient… unless viewed as a precursor to paper tape punch or magnetic tape recording.

Berry’s M.S. thesis was to find a combination of these competing design variables that works. He found it. The write voltage was 3,000 V, and the read voltage is 2,000 V. With it, the ABC is able to record the entire contents of one memory drum (1500 bits) in one second. It would be many years before there was another method capable of this I/O rate. The scratch paper cards were about 12 cm by 18 cm and were loaded individually. As they ejected from the mechanism, they were apparently caught by hand; there is no record of any kind of tray.

Burks [2] cite the reliability of the arcing scheme as roughly one error in every 10⁴ or 10⁵ bits. This is high, but probably not high enough for the solution of 29 equations in 29 unknowns. The likelihood of a one-bit error increases rapidly beyond about five equations in five unknowns, and this may be the source of the debate, “Did the Atanasoff-Berry Computer ever work?” From hands-on experience, we can now give the answer: yes, but reliability problems prevented it from solving systems large enough to fill its memory. It was still much faster and more reliable than hand calculation, which is what Atanasoff had hoped to achieve.

7. The ABC “Instruction Set”

The operator invokes “instructions” via the buttons and switches on the control panel. A vector is a set of the 30 numbers in either memory drum. (The vector in memory 1 is called CA in earlier descriptions of the ABC, and the vector in memory 2 is called KA.) A short vector is five numbers, aligned to end on a multiple of 5 within the vector; a decimal input card held one short vector, whereas the binary scratch cards held an entire vector. The possible instructions, with approximate execution times, are as follows:

1 s Set short vector to coefficients 1 to 5.

1 s Set short vector to coefficients 6 to 10.

1 s Set short vector to coefficients 11 to 15.

1 s Set short vector to coefficients 16 to 20.

1 s Set short vector to coefficients 21 to 25.

1 s Set short vector to coefficients 26 to 30.

1 s Vector clear memory 1.

1 s Vector copy memory 1 to memory 2.

16 s Read a short vector from the base-10 card reader into part of the memory 1 vector, converting to binary using table look-up and the add-subtract modules.

1 s Read a short vector from the base-2 card reader into part of the memory 1 vector.

1 s Read a short vector from the base-2 card reader into part of the memory 2 vector.

1 s Select a coefficient in memory 1 (for elimination or decimal output).

100 s Add or subtract (chosen automatically) one row from another to eliminate the leading bit of the chosen coefficient, shifting right when successful and stopping when the chosen coefficient is zero.

100 s Write a value to the decimal readout, using the lookup tables and add-subtract modules to convert the base-2 value to base-10.

The timings of more than 1 second are data-dependent, and the values given represent averages for 15-decimal numbers. By using small integers instead of the full dynamic range, the time for those long operations drops by an order of magnitude.

A striking omission in the design of the ABC is the concept of addressing. Binary data is not used anywhere to select data locations. The operator performed the selection, which is why the design has so many sizes that are not powers of two (such as 5, 30, 50, 1500).

8. Base-10 Output

Descriptions were frustratingly sketchy when describing where the answers finally appeared in human-readable form. We knew that Berry had attempted to use a car odometer to record the output, but eventually custom-made what he needed. The black-and-white photographs of the machine did not reveal anything obviously intended for the output, and we had to solve this mystery before reconstruction could begin.

The man who took those photographs was also the man who did most of the wiring of the original ABC: Dr. Robert Mather. Mather, a physicist living in Oakland, California, is perhaps the only person still living that saw the ABC in operation. (Atanasoff was alive when the reconstruction project began, but had suffered several strokes and was unable to communicate with us). We contacted Mather, who pointed out the cylinder next to the base-10 card reader in the photograph, and all became clear. The same mechanism that moved the card reader could be used to move a solenoid past odometer-type wheels, poking them by one decimal every time a value on the drum with the conversion table subtracted that decimal. Unlike a car odometer, there is no “carry” when a wheel passes 9; the wheels are independent. The display is small, since it has the same spacing as columns on an IBM punch card.

Because the algorithm alternates between adding and subtracting as the solenoid moves across columns of the number, the wheels are numbered in alternating forward and reverse order. This simplifies the mechanical aspects of the conversion, since the solenoid always moves the same way but the electronics change state.

One does not find clear answers to some questions in the literature on the ABC. I will attempt to answer those now, based on our experience with the replica and the additional sources of information we found in our quest for details about the original.

9. Exactly When Was It Completed?

Unlike an invention like the Wright Brothers’ airplane, we do not have a precise date in history for the first successful electronic computation. There does not seem to be a precise date when one can say the ABC worked for the first time. The binary logic certainly was working by the summer of 1940, but the base-2 scratch storage method described above became reliable enough to use as a gradual process and not a dramatic one. By the time World War II had taken everyone away from the project in June 1942, the ABC was in the state that we have reproduced, and that reproduction is a working computer.

Had the war not interfered, Atanasoff was planning to make the instruction sequencing automatic instead of entered manually from the control panel, and to make the computer more general-purpose. With the exception of Zuse’s paper-tape mechanism for instruction sequences, stored instruction sequencing had to wait until the late 1940s.

10. Was the ABC Electronic or Electromechanical?

The fractional-horsepower motor and gear trains suggest that the ABC was an electromechanical computer and not an electronic one. This is not the case. The mechanical function was similar to the motor that turns the hard disk or CD-ROM drive inside a modern computer; the gears and mechanical parts were not used for computing or to record data in any way.

A small number of relays were used, but only for control. They more closely resemble the on-off switch on a modern PC than the gate elements of the Zuse Z3.

Modern electronic computers have many moving parts in the input keyboards and output printers, and so did the ABC. It is true that the clocking of the system was mechanical and not electronic. With an oscillatory circuit used to set the system clock instead of a rotating cylinder making contact with brushes, the ABC logic could have been made ten thousand times faster. Note, however, that this would have been a gross mismatch to the I/O limitations of the system. Even the later ENIAC, which used electronic clocking, experienced its bottleneck in the punch card input and output.

The ABC was fully electronic in its calculation and in its storage of data. For that reason, I argue that its mechanical aspects are no different from those of any modern computer; a motor to rotate the storage medium, and mechanical switches for the human interface.

11. Was the ABC Ever Actually Used?

Some have claimed that no one ever used the original ABC for production computing. We have found evidence to the contrary. The first three applications listed by Atanasoff are all statistical, and Atanasoff collaborated with the well-known applied statistician Snedecor at ISU. Publicity that resulted from our reconstruction effort led Clara Smith, a secretary in the Mathematics Department now living in rural Iowa, to contact us. She said one of her tasks was to hand-verify solutions to problems that Snedecor was sending to Atanasoff. It appears Snedecor sent a steady stream of small linear systems to the ABC for solution, and it would have been very well suited to regression, least squares, curve-fitting problems. Clara Smith verified some of the results for Snedecor to establish his confidence that the ABC was producing correct answers.

Robert Mather also says the original machine solved problems up to size five, but more typically size three during testing and debugging. The experience we have had with the replica makes this recollection very plausible. Five is the size of a “short vector” that fits on one input card, and does not require any switches to be changed on the short vector location. It also involved about 3 × 10⁴ bits to be sent through the base-2 mass storage system, which is about where the reliability of that system becomes limiting. A linear system size of three is very useful in testing and debugging, since one can solve a 2 by 2 system plus right-hand-side vector without any use of scratch storage. Since we have done nothing to improve on the technology of the original, I feel we have settled the question of whether the original ABC was ever operational: It was. Moreover, it was probably used to solve real statistical problems.

12. How fast was the ABC?

As in all computer performance measurement, it is better to take into account the time to solve an entire problem and not excerpt the time to do a single operation as a measure of speed. The latter is usually much more flattering, but seldom reflects true performance. For example, one could cite the fact that a 30-element vector addition on the ABC takes only one second, implying 30 arithmetic operations per second. Perhaps this is the “peak performance” rating for the ABC. I instead consider “sustained performance.” To measure that, there is no substitute for a working replica.

Because of the parallelism in the architecture, the sustained performance is maximized if all 30 add-subtract units are used; that is, if one solves a system of 29 equations in 29 unknowns. Burks has estimated that this would take about 25 hours, including human operator time [2]. With a LINPACK-type operation count of ²⁄3N³ + 2N², the Gaussian elimination of a system of size 29 requires about 18,000 operations. This implies 0.2 operations per second. Because the ABC had parallelism greater than N, the time complexity grows as N² and not N³.

I have noted that the ABC probably never was used for such a large system because of the very high reliability requirements for the scratch storage. We can look at the other extreme, two equations in two unknowns. The usual floating-point operation count for a 2 by 2 system (counting reciprocation as three operations) is 19. Our experience is that such a problem can be solved in about five minutes, somewhat less than the estimate in the Burks’ book. This implies 0.06 operations per second. The 2 by 2 system need not involve scratch storage, which saves time beyond what would expect from problem scaling.

13. How “Special-Purpose” was the ABC?

Some refer to the ABC as a “special-purpose” computer, perhaps to diminish its place in computer history. “Special-purpose” and “general-purpose” are not scientifically defined adjectives. Most computers are designed with a certain range of applications in mind, and the list that Atanasoff mentions above is broad. We already know that the ABC did not have an automatic instruction stream like the Harvard Mark I; its only capacity for branching was in testing zero crossings and zero results during elimination. It relied on the human operator to deliver commands and make decisions about what to do next.

After the ABC reconstruction began to be operational, I realized that the ABC could in fact be employed the way one would use a pocket calculator, and that it could be “programmed” in a sense by the choice of matrix coefficient data. To see this, consider what happens when one solves the system

ax + by = u

cx + dy = v

The result of one application of the ABC row-elimination step results in

ax + by = u

0 + (d – bc/a)y = v – uc/a)

The quantity (d – bc / a) is easily read out on the decimal display. Quantities u and v need not even be entered. If we want to obtain the four basic operations + – × ÷, then

b = –1, a = +1 gives c + d.

b = +1, a = +1 gives d – c.

d = 0, a = –1 gives b × c.

d = 0, c = –1 gives b ÷ a.

Although this may seem clumsy, it was certainly easier and less error-prone than doing 15-decimal arithmetic by hand.

14. Perspective: Computers Now and Computers Then

The ABC illustrates two remarkable things about the history of computers: First, that Moore’s law seems to work if extrapolated all the way to 1939, and second, that a surprising number of things have not changed much from the ABC.

Moore’s law was first posited in 1970, using only three data points. It primarily applied to chip density, and by implication the cost per bit… but because speed tends to scale linearly with memory, it has been found to be a good guideline for processor speed as well: Performance doubles every 18 months. So if we extrapolate back to 1942 from say, late 1996, we should have doubled performance about 36 times. 2³⁶ is about 70 billion (American system, billion = 10⁹). Are current supercomputers 70 billion times more capacious and faster than the ABC? Does Moore’s law hold even before the invention of integrated circuits?

The ABC had 0.3 kilobytes of main storage. The Intel Teraflops computer delivered to Sandia National Laboratories last year now has 0.3 terabytes of main memory and a terabyte of disk storage. It isn’t clear which one we should use, because the ABC memory used refreshed capacitors like DRAM yet spun mechanically like a disk. The speed of the ABC was, translated to modern terms, about 0.06 “FLOPS” where we politely ignore the lack of exponent management in the ABC and look at the 50-bit precision as similar to a modern 52-bit IEEE mantissa. The Intel Teraflops computer, true to its name, has demonstrated a trillion FLOPS with that precision, and running the same application. That represents a factor of about 20 trillion.

With this improved baseline, we can recalibrate Moore’s law… but it doesn’t need much modification. It looks like DRAM technology doubles every 20 months, and processor speed doubles every 28 months. It’s a little like recalculating the Hubble Constant when a telescope finds another more ancient and more distant quasar.

15. Cost

If the reader will forgive my use of American units, someone once noted that computers cost about $400 per pound… give or take $100. This amusing statistic is surprisingly good at predicting the cost of everything from a pocket calculator (0.1 pound, $40) to a Cray vector mainframe (30,000 pounds including motor-generators, $12,000,000). While we’d like to think that the cost of a computer stems from its intellectual content and not its mass, the heuristic seems to work. The ABC weighs 750 pounds, and it cost about $300,000 to reconstruct. This fits the $400/pound estimator despite the use of vacuum tube technology. This ABC price includes the engineering labor cost; some quoted prices for the original ABC list $5000, and include only the parts in 1939 dollars. If one adjusts for inflation and estimates the cost of Atanasoff, Berry, and the several students that helped with the original, the cost of the reconstruction is very close to the price of the original.

16. Summary

Scientific computer architectures have long been designed with linear algebra in mind. The vector computers of the late 1970s and early 1980s (CRAY-1, CYBER 205, etc.) and array processors of the same era were strongly optimized for the kernel operations of matrix factoring and matrix multiplication. The ABC was the first linear algebra computer, and its 1940 performance is very close to what Moore’s law predicts. World War II prevented its innovations from being publicized and credited to Atanasoff and Berry via patents or published papers. However, the ideas of fully electronic digital logic and dynamic refresh capacitor storage were communicated to other early designers and were thereby added to the body of knowledge of computer design.

Acknowledgments

The reconstruction of the ABC was driven initially by two men: Delwyn Bluhm, Manager of Engineering Services at Ames Laboratory, and George Strawn, former director of the Iowa State University Computation Center. They obtained initial funding from Charles Durham, a successful executive who had been a student of John Atanasoff. Without the enthusiasm and vision of Bluhm and Strawn, the ABC reconstruction would not have happened. Engineers Gary Sleege, Dave Burlingmair, John Erickson, and many others worked long and hard to reproduce what Atanasoff and Berry had created over 50 years earlier. The entire project was privately funded; no government money was used.

The person who took the replica from a mere look alike to a functioning computer was Charles Shorb, a dedicated graduate student and as close to a modern-day Clifford Berry as one could ask for. Mr. Shorb had worked on the Intel Teraflops computer just prior to his work finishing the ABC, so he went from the world’s fastest computer to the world’s slowest one (a ratio of about 10¹³:1). When the press release went out from Intel that its parallel processor had demonstrated over a trillion operations per second, the problem that it solved was one Atanasoff would have appreciated had he lived to see it: It solved a linear system of 125,000 equations in 125,000 unknowns.

References

A web site with information about the ABC and the reconstruction effort can be found at http://www.scl.ameslab.gov/ABC.

[1] J. V. Atanasoff, “Advent of Electronic Digital Computing,” Annals of the History of Computing, Volume 6, Number 3, July 1984.

[2] A. R. and A. W. Burks, The First Electronic Computer: The Atanasoff Story, University of Michigan Press, Ann Arbor, 1989.

[3] J. L. Gustafson, “First Electronic Digital Calculating Machine Forerunner to Cornell’s FPS-164/MAX,” Forefronts, Cornell University Theory Center, October 1985.

[4] A. R. Mackintosh, “Dr. Atanasoff’s Computer,” Scientific American, August 1988.

[5] C. R. Mollenhoff, Atanasoff: Forgotten Father of the Computer, Iowa State University Press, Ames, 1988.

[6] B. Randell, The Origins of Digital Computers, First Edition, Springer-Verlag, New York, 1973.

[7] R. Rojas, “Sixty Years of Computation — The Machines of Konrad Zuse,” Preprint SC 96–9, Konrad-Zuse-Zentrum für Informationstechnik Berlin, Heilbronner Str. 10, D-10711 Berlin-Wilmersdorf, March 1996.

__________

PROF. JOHN GUSTAFSON is a Computational Scientist at Ames Laboratory in Ames, Iowa, where he is working on various issues in high-performance computing. He has won three R&D 100 awards for work on parallel computing and scalable computer benchmark methods, and both the inaugural Gordon Bell Award and the Karp Challenge for pioneering research using a 1024-processor hypercube. Dr. Gustafson received his B.S. degree with honors from Caltech and M.S. and Ph.D. degrees from Iowa State, all in Applied Mathematics. Before joining Ames Laboratory, he was a software engineer for the Jet Propulsion Laboratory in Pasadena, Product Development Manager for Floating Point Systems, Staff Scientist at nCUBE, and Member of the Technical Staff at Sandia National Laboratories. He is a member of IEEE and ACM.